What is Raman Spectroscopy?

Apollo M™ Raman microspectrometer
Raman Microspectrometer Design
Uses of Micro Raman Spectrometers
Units of Micro Raman Spectroscopy
CRAIC Apollo™ MicroRaman Spectrometer
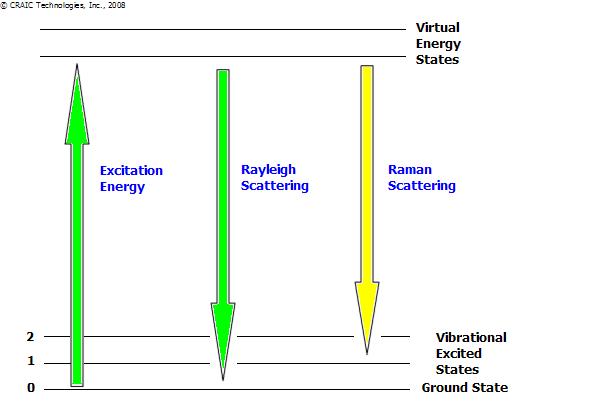
Energy Level Diagram Depicting Raman Scattering
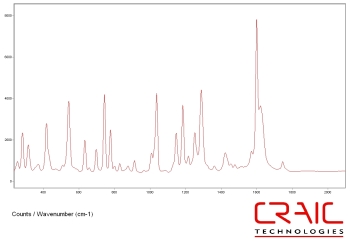
Raman spectra of Aspirin
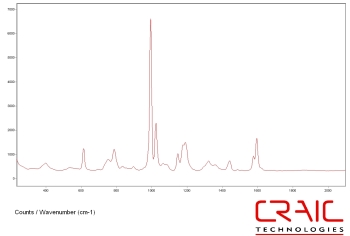
Raman spectra of polystyrene
When electromagnetic energy interacts with a material, it can either be reflected, absorbed, transmitted, or scattered. One type of scattering is Raman scattering and is the basis for Raman spectroscopy. Raman spectroscopy is useful as the Raman scattered light yields data of the vibrational modes of the sample molecules. A Raman spectrum thus enables the identification of molecules and their functional groups, similar to IR spectroscopy, but with visible range light.
Raman Scattering
Raman spectroscopy is the study of the interaction between light and matter where light is inelastically scattered: a process upon which Raman spectroscopy is based.
During an experiment using Raman spectroscopy, light of a single wavelength is focused onto a sample. Most commonly a laser is used as it is a powerful monochromatic source. The photons from the laser interact with the molecules of the sample and are scattered inelastically. The scattered photons are collected and a spectrum is generated from the scattered photons.
Photons interacting with molecules most commonly scatter elastically. This is called Rayleigh scattering. Rayleigh scattered photons have the same wavelength as the incident light. However, approximately 1 out of a million photons are inelastically scattered...an effect first described by Sir Chandrasekhara Raman in 1922. This is the principle from which Raman spectroscopy derives.
With Raman scattering, the incident light interacts with matter and its wavelength is either shifted lower or higher (red or blue shifted, respectively). Red shifted photons are the most common, having been subject to a "Stokes shift". What has happened is that the photon has interacted with the electron cloud of the functional groups bonds, exciting an electron into a virtual state. The electron then relaxes into an excited vibrational or rotational state (see the diagram). This causes the photon to lose some of its energy and it is detected as Stokes Raman scattering. This loss of energy is directly related to the functional group, the structure of the molecule to which it is attached, the types of atoms in that molecule and the molecule's environment.
Of course, not every molecule or functional group exhibits Raman scattering. The following factors influence Raman scattering:
- The polarization state of the molecule (which determines the Raman scattering intensity) must be considered.
- The greater the change in polarizability of the functional group, the greater the intensity of the Raman scattering effect.
This means that some vibrational or rotational transitions, which exhibit low polarizability, and will not be Raman active. They will not appear in a Raman spectra.
Micro Raman Spectroscopy
Raman microspectroscopy is where a Raman microspectrometer is used in place of a standard Raman spectrometer. A Raman microspectrometer consists of a specially designed Raman spectrometer integrated with an optical microscope. This allows the experimenter to acquire Raman spectra of microscopic samples or microscopic areas of larger samples. The advantages are that much less samples is required and certain effects may also be enhanced over very localized regions.
Resonance Raman Spectroscopy
It should be noted that Raman scattering is a very weak effect as most photons are Rayleigh scattered. However, the intensity of the effect can be dramatically increased using resonance Raman spectroscopy. In resonance Raman spectroscopy, the wavelength of the exciting laser light coincides with the absorbance maximum of the molecule or functional group. Therefore, the photon can excite an electron to near an electronic excited state rather than a virtual excited state. This results in an increase in the Raman scattering intensity by a factor up to a million. This transition is therefore dominant in the resultant Raman spectrum: the Raman spectrum is of the molecule whose absorbance corresponds to the wavelength of the laser. This is why Raman microspectrometers are often offered with multiple lasers with differing laser wavelengths: different samples may be excited at different wavelengths in order to obtain the strongest Raman signal.
Surface Enhanced Raman Spectroscopy
Surface enhanced Raman spectroscopy (SERS) is another method of signal enhancement for Raman spectroscopy. The most important factor of this technique is sample preparation. Sample molecules are adsorbed onto specially prepared metal surfaces. These surfaces are "rough" on the nanoscale and are usually either gold or silver. Raman spectra can then be taken using standard methodologies but with signal enhancement of approximately a trillion. However, the correct laser wavelength must be selected that best interacts with the metal surface in order to see the SERS effect.

